| 發布者 | 內容列 |
zaq1bgt5cde3mju7
Home away from home


註冊日: 2010-04-03
發表數: 559
台灣台中市
|  特別的機率問題(5) 特別的機率問題(5) |  | 甲乙兩人玩猜拳,猜贏得一分
一直猜到猜拳平手為止
然後結算分數
求甲乙同分的機率為何??
_________________
思考數學------"樂趣"與"收穫"都能兼得
|
|
 2011-03-03 22:47 2011-03-03 22:47 |   |
d22538366
Home away from home


註冊日: 2010-12-25
發表數: 176
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 偶數次的時候機率是0嗎 |
|
 2011-03-06 01:27 2011-03-06 01:27 |   |
zaq1bgt5cde3mju7
Home away from home


註冊日: 2010-04-03
發表數: 559
台灣台中市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
d22538366 寫道:
偶數次的時候機率是0嗎
是啊,但奇數次呢??
我還沒解出來
解出後還有更難的問題已經想好了
_________________
思考數學------"樂趣"與"收穫"都能兼得
|
|
 2011-03-06 10:26 2011-03-06 10:26 |   |
ricktu
Home away from home


註冊日: 2009-08-23
發表數: 179
台北市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 於第3次平手時,同分的機率為2/4=1/2
於第5次平手時,同分的機率為6/16=2/5
於第7次平手時,同分的機率為20/64=5/16
是嗎
(於第n次平手時,同分的機率為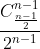 ) )
_________________
01010010011010010110001101101011001000000101010001110101
|
|
 2011-03-06 16:41 2011-03-06 16:41 |  |
zaq1bgt5cde3mju7
Home away from home


註冊日: 2010-04-03
發表數: 559
台灣台中市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
ricktu 寫道:
於第3次平手時,同分的機率為2/4=1/2
於第5次平手時,同分的機率為6/16=2/5
於第7次平手時,同分的機率為20/64=5/16
是嗎
是
如果這樣算,那等於求一個無窮級數的和
f(n+1)=[(4n+2)/(9n+9)]f(n),f(0)=1/3
求無窮級數f(0)+f(1)+f(2)+...=??
怎麼解啊??
_________________
思考數學------"樂趣"與"收穫"都能兼得
|
|
 2011-03-06 19:11 2011-03-06 19:11 |   |
ricktu
Home away from home


註冊日: 2009-08-23
發表數: 179
台北市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 答案不能用無窮級數表示嗎?
如果是收斂的無窮級數,那答案就是它的極限阿
_________________
01010010011010010110001101101011001000000101010001110101
|
|
 2011-03-06 19:32 2011-03-06 19:32 |  |
zaq1bgt5cde3mju7
Home away from home


註冊日: 2010-04-03
發表數: 559
台灣台中市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
ricktu 寫道:
答案不能用無窮級數表示嗎?
如果是收斂的無窮級數,那答案就是它的極限阿
應該也可以啦
但是這個無窮級數一定收斂
能求出來更好,雖然變得跟機率扯不上關係......
_________________
思考數學------"樂趣"與"收穫"都能兼得
|
|
 2011-03-07 07:36 2011-03-07 07:36 |   |
hansonyu123
Home away from home


註冊日: 2010-11-28
發表數: 506
台灣
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
zaq1bgt5cde3mju7 寫道:
引文:
ricktu 寫道:
於第3次平手時,同分的機率為2/4=1/2
於第5次平手時,同分的機率為6/16=2/5
於第7次平手時,同分的機率為20/64=5/16
是嗎
是
如果這樣算,那等於求一個無窮級數的和
f(n+1)=(4n+2)/(9n+9),f(0)=1/3
求無窮級數f(0)+f(1)+f(2)+...=??
怎麼解啊??
為什麼這個無窮級數是這樣啊?
看不出哪裡一樣
_________________
去吧!神奇數學球!
--------------------------------------------------------------
金
字塔
也應該
要有進步
的這一天吧
今天我就讓他
徹徹底底進化吧
二零一二零九二九
二一點二六分三十秒
不要問我現在是幾毫秒
|
|
 2011-03-07 20:20 2011-03-07 20:20 |  |
hansonyu123
Home away from home


註冊日: 2010-11-28
發表數: 506
台灣
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 另外
這個數列的總和是無限
因為可以將f(n+1)改成
f(n+1)=4/9 + 2/(9n+9)
當n趨近於無限時,f(n+1)趨近於4/9
且n+1趨近於無限,f(n+2)趨近於4/9……………
所以這個無窮級數的和>4/9*無限=無限
_________________
去吧!神奇數學球!
--------------------------------------------------------------
金
字塔
也應該
要有進步
的這一天吧
今天我就讓他
徹徹底底進化吧
二零一二零九二九
二一點二六分三十秒
不要問我現在是幾毫秒
|
|
 2011-03-07 20:34 2011-03-07 20:34 |  |
zaq1bgt5cde3mju7
Home away from home


註冊日: 2010-04-03
發表數: 559
台灣台中市
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
hansonyu123 寫道:
另外
這個數列的總和是無限
因為可以將f(n+1)改成
f(n+1)=4/9 + 2/(9n+9)
當n趨近於無限時,f(n+1)趨近於4/9
且n+1趨近於無限,f(n+2)趨近於4/9……………
所以這個無窮級數的和>4/9*無限=無限
打錯了,上面已修正
_________________
思考數學------"樂趣"與"收穫"都能兼得
|
|
 2011-03-07 20:43 2011-03-07 20:43 |   |
hansonyu123
Home away from home


註冊日: 2010-11-28
發表數: 506
台灣
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 引文:
zaq1bgt5cde3mju7 寫道:
引文:
hansonyu123 寫道:
另外
這個數列的總和是無限
因為可以將f(n+1)改成
f(n+1)=4/9 + 2/(9n+9)
當n趨近於無限時,f(n+1)趨近於4/9
且n+1趨近於無限,f(n+2)趨近於4/9……………
所以這個無窮級數的和>4/9*無限=無限
打錯了,上面已修正
請問
「 [ ] 」是指中括號還是高斯符號?
_________________
去吧!神奇數學球!
--------------------------------------------------------------
金
字塔
也應該
要有進步
的這一天吧
今天我就讓他
徹徹底底進化吧
二零一二零九二九
二一點二六分三十秒
不要問我現在是幾毫秒
|
|
 2011-03-07 21:27 2011-03-07 21:27 |  |
hansonyu123
Home away from home


註冊日: 2010-11-28
發表數: 506
台灣
|  Re: 特別的機率問題(5) Re: 特別的機率問題(5) |  | 無窮級數改成這樣子會不會更好?
f(n+1)=(2n-1)/(8n)*f(n) f(1)=1/3
求f(1)+f(2)+………的和?
_________________
去吧!神奇數學球!
--------------------------------------------------------------
金
字塔
也應該
要有進步
的這一天吧
今天我就讓他
徹徹底底進化吧
二零一二零九二九
二一點二六分三十秒
不要問我現在是幾毫秒
|
|
 2011-03-07 21:52 2011-03-07 21:52 |  |
d22538366
Home away from home


註冊日: 2010-12-25
發表數: 176
| |
 2011-03-08 00:34 2011-03-08 00:34 |   |
hansonyu123
Home away from home


註冊日: 2010-11-28
發表數: 506
台灣
| |
 2011-03-08 18:24 2011-03-08 18:24 |  |

